Big-O notation

Big-O notation categorizes algorithms based on efficiency. It helps us compare and choose the best algorithm for a task.

The Essence of Big-O

One way of finding the largest number in a list involves comparing each number to the current largest one. This is a linear time algorithm, shown as O(n).

Another approach involves dividing the list in half, finding the largest numbers in each half, and comparing them. This is more efficient and represents a logarithmic time algorithm, shown as O(log n).

Understanding Big-O notation is important for several reasons:

1. Performance Optimization: It helps predict the impact of increasing input size on algorithm performance.
2. Algorithm Comparison: Provides a standardized way to compare the efficiency of different algorithms.
3. Code Scalability: Helps design and implement scalable solutions for large datasets.

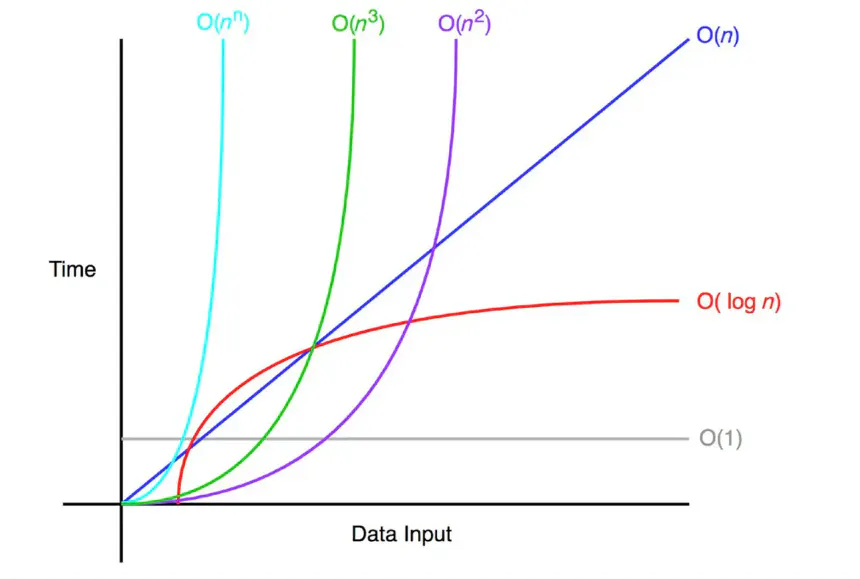
Common Big-O Notations

O(1): Constant time. The algorithm takes the same amount of time regardless of input size.

O(log n): Logarithmic time. The runtime grows logarithmically with input size.

O(n): Linear time. The runtime grows linearly with input size.

O(n log n): Log-linear time. The runtime grows slightly faster than linear time.

O(n^2): Quadratic time. The runtime grows quadratically with input size.

O(2^n): Exponential time. The runtime grows exponentially with input size.

Big-O notation gives a good idea about algorithm efficiency, but doesn't cover everything. Factors like constant factors and specific hardware also affect performance. Still, it's useful for understanding algorithm scaling and making smart choices.

Understanding Big-O helps us pick efficient algorithms, improve code, and handle big datasets.